Different methods for completing the Binomial Tree

CFA Level II Fixed Income
#1

I) Kaplan Vol. 2, Exam 3 AM excerpt:

Mike Diffle has been asked to evaluate the bonds of Hardin, Inc. The specific issue Diffle is considering has an 8% annual coupon and matures in two years. The bonds are currently callable at 101, and beginning in six months, they are callable at par. Bratton Corporation, Hardin’s competitor, also has bonds outstanding which are identical to Hardin’s except that they are not callable. Diffle believes the AA rating of both bonds is an accurate reflection of their credit risk. Diffle is wondering if the Bratton bonds might be a better investment than the Hardin bonds. Assume that the following 1-year interest rate tree is used to value bonds with a maturity of up to three years (this tree assumes interest rate volatility of 10%).

Today=7.25%

Yr 1: U=8.53% D=6.983%

Yr 2: UU=9.324% UD=7.634% DD=6.25%

Also, assume that the appropriate spot rates for securities maturing in one, two, and three years are 7.25%, 7.5%, and 7.80%, respectively.

Q : Calculate the value of the Bratton bonds using the interest rate tree.

Solution: Interest rate tree: Discount maturity value back one year at different 1-year forward rates, then take the equally weighted average of those values discounted back to today at today’s 1-year rate:

V = 0.5 × [(108 / 1.08530) + 8] / 1.0725 + 0.5 × [(108 / 1.06983) + 8] / 1.0725

V = 0.5 × (99.512 + 8) / 1.0725 + 0.5 × (100.951 + 8) / 1.0725

V = 50.122 + 50.793 = 100.915

In other words:

V 1,U=107.12

V 1, D=108.951

V0=100.915

II) Kapaln V2 Exam 2 PM Question #43:

Exhibit 2:

Bond A Coupon 5%, annual pay Par Value:100 Type:Option-Free Maturity:3 years

Exhibit 1: Binomial Interest Rate Tree (σ = 10 %, annual pay)

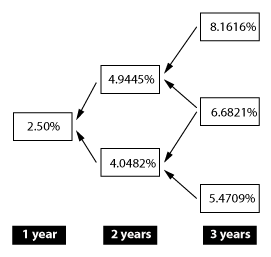
Using the information in Exhibits 1 and 2, the value of bond A is closest to:

The completed binomial tree is as follows:

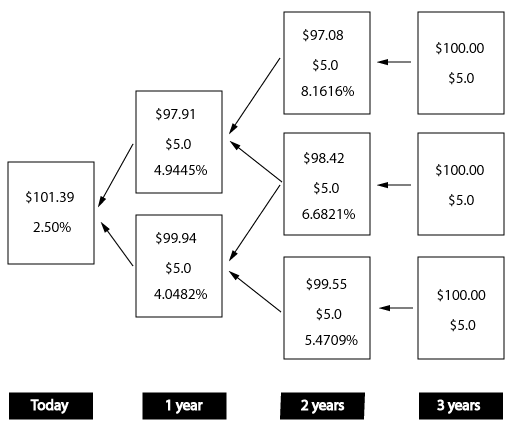
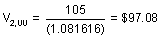
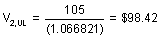
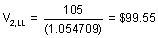
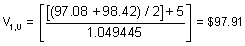
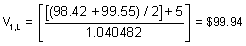
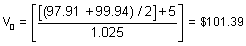
My dilemma :

In the first example we’re adding the coupon to the current discounted cash flow from the previous node, in order to get the PV of the Bond (CF+current coupon, the coupon doesn’t get discounted at the present node as it is already in the PV terms for that particular node.

Ex: V 1,U= [(108 / 1.08530) + 8]=107.51

In the second example, we do not add the current coupon to get the current value of the bond at that particular node.

Ex: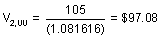

I’ve come across the very same discrepancy in Wiley vs. CFAI material and posted in on here; however, have not received a response =( I’m pulling my hair out on this, is anyone able to assist please?

#2

I think in the first example we are given the following information" assume that the following 1-year interest rate tree is used to value bonds". Because it is only a one-year tree, we basically ignore any values beyond year 1.

I would think that must be the explanation.

#3

This is crushing me as well…

#4

Same with me, I posted about it too, but noone seems to have the solution.

In CFAI the difference is btw readings 36 and 37.

#5

The only thing I could figure out, that if we add the coupon to create the value, all values would be higher so most callable bonds would be called, putable bonds almost never (assuming exercise price is somewhere around par), so for bonds with embedded options I would not add.

However in CFAI EOC in reading 36 (value bonds w/o options) one of the wrong answers was where they did not add the coupon.

#6

There was a thread on this before but I wasn’t able to reconcile like these guys did:

https://www.analystforum.com/forums/cfa-forums/cfa-level-ii-forum/91340274