TVM - Annuity due Help on Practice Problem

CFA Level I Quant
#1

Q: A couple plans to pay their child’s college tuition for 4 years starting 18 years from now. The current annual cost of college is C$7,000, and they expect this cost to rise at an annual rate of 5 percent. In their planning, they assume that they can earn 6 percent annually. How much must they put aside each year, starting next year, if they plan to make 17 equal payments?

Solution:

The correct answer is C$2,221.58.

  1. Draw a time line. CFA0123-P-S19i.png
  2. Recognize that the payments in Years 18, 19, 20, and 21 are the future values of a lump sum of C$7,000 in Year 0.
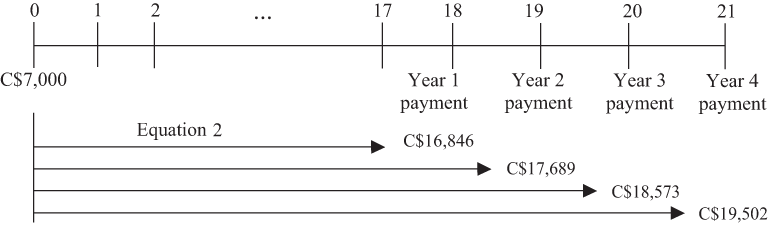
  3. With r = 5%, use the formula for the future value of a lump sum (Equation 2), FV_N_ = PV (1 + r)N, four times to find the payments. These future values are shown on the time line below. CFA0123-P-S19iii.png
  4. Using the formula for the present value of a lump sum (r = 6%), equate the four college payments to single payments as of t = 17 and add them together. C$16,846(1.06)−1 + C$17,689(1.06)−2 + C$18,573(1.06)−3 + C$19,502(1.06)−4 = C$62,677
  5. Equate the sum of C$62,677 at t = 17 to the 17 payments of X, using the formula for the future value of an annuity (Equation 7). Then solve for X. C$62,677=X[(1.06)17−10.06]=28.21288XX=C$2,221.58 Notation Used on Most Calculators** Numerical Value **for This Problem N 17 %i 6 PV n/a (= 0) FV C$62,677 PMT compute X CFA0123-P-S19v.png In summary, the couple will need to put aside C$2,221.58 each year if they start next year and make 17 equal payments.

Is there a more time efficient way of doing step 4 in a calculator? I am using Texas BI BAII Plus. Does one have to find all the FV of the $7000 & then find the PV of these at t17 ?

I am really struggling to understand this Solution.

#2

Use the C.F. worksheet to get the pv at time 0 of the projected tuition amounts. cf0=0, c01=0, f01=17, c02=16846, f02=1, etc. Use NPV worksheet @ 6% which produces $23,276.104.

Use tvm worksheet n=17 i=6 pv=23,276.104 cpt pmt -2,221.58. of course p/y=c/y=1 and use END.

ETA: focal date in part 1 is time 0.

1 Like
#3

N.B.: $23,276.104 × 1.04^17 = $62,677. :bulb:

#4

Thanks for your quick response. So I do need to calculate the Projected Tuition amounts at each t from 18 -> 21? Note them and then key them back in to the calculator in the NPV worksheet?

Appreciate your help. I am new to this.

#5

I have tried using the CF Worksheet to get to £23,276.10 but I can’t - I am getting $50,390.32. I’m begining to understand this problem. Thanks again

#6

I GET IT.

Thank you so much breadmaker. I finally figured out where I was going wrong.

#7

:slightly_smiling_face: :+1:

You do have to explicitly project out the nominal amounts for years 18-21 inclusive. Use the calcs below to duplicate the method in the solution (using time 17 as as the focal date):

CF0 =0 CF1=16,846 F01=1,…C04=19,502 F04=1 NPV I=6 CPT PV 62677

N=17 I=6 FV 62677 CPT PMT -2,221.58

#8

The PV comes to 23276? & then work out for FV @ t17 = 62677. You have confused me again!! Ha

I used ANS in CF1 to get the 16,846 and then in CF2 I did ANS x 1.05 … and so on.

#9

If mom and dad have $23,276 lying around when Junior is born, it will roll up with interest @6% annually over 17 years to $62,677. It’s two different ways of looking at the same problem.

You can also use the TVM worksheet to get the nominal tuition amounts. N=18, 19, 20, 21 I=5% PV=7,000 CPT FV -16846.33, -17688, etc.

#10

Perfect Thank you.

I am stuck again - Can’t seem to figure out my misstep. Another CF problem:

Q: A saver deposits the following amounts in an account paying a stated annual rate of 4%, compounded semiannually:

Year** End of Year Deposits ($)** 1 4,000 2 8,000 3 7,000 4 10,000

Q. At the end of Year 4, the value of the account is closest to:

  1. $30,432
  2. $30,447
  3. $31,677
    Solution:

B is correct. To solve for the future value of unequal cash flows, compute the future value of each payment as of Year 4 at the semiannual rate of 2%, and then sum the individual future values, as follows:

Year** End of Year Deposits () ****Factor**** Future Value ()** 1 4,000 (1.02)6 4,504.65 2 8,000 (1.02)4 8,659.46 3 7,000 (1.02)2 7,282.80 4 10,000 (1.02)0 10,000.00 Sum = 30,446.91

I enter CFo = 0 , C01 = 4,000 F01 = 1 … C04 = 10,000 F04 = 1 I = 4/2 = 2 I am getting 27,445.63 Again, do I need to just work all four out ‘manually’, jot them down and then sum them?

Really appreciate your help, also new to this forum so if this is not the right place for this - I’m all ears.

#11

You can use the TVM worksheet with P/Y=1 and C/Y=2 to accumulate each individual deposit. For the first deposit N=6, I=4 PV= 4,000 CPT FV -4,504.65. Set N and PV appropriately for all the other deposits and sum up the FVs.

You can use the CF worksheet as well. Keep your C’s and F’s the same, but set I as 1.02^2-1 =0.0404 (4.04%). Compute the NPV and multiply it by 1.02^8.